


ade4 in 
|
|
|
Exploratory and Euclidean methods in Environmental sciences |
|
| Welcome | adelist | Teaching | Gallery | Documentation | Downloads | Rweb | Links | ChangeLog |
Article Rnews 2004The ade4 package - I : One-table methodsby Daniel Chessel, Anne B Dufour and Jean Thioulouse
Chessel, D., A.-B. Dufour, and J. Thioulouse. 2004. The ade4 package-I- One-table methods. R News 4:5-10.
Introduction The duality diagram class Distance matrices Taking into account groups of individuals Permutation tests Conclusion 1 IntroductionThis paper is a short summary of the main classes defined in the ade4 package for one table analysis methods (e.g., principal component analysis). Other papers will detail the classes defined in ade4 for two-tables coupling methods (such as canonical correspondence analysis, redundancy analysis, and co-inertia analysis), for methods dealing with K-tables analysis (i.e., three-ways tables), and for graphical methods. This package is a complete rewrite of the ADE4 software ([Thioulouse et al., 1997], http://pbil.univ-lyon1.fr/ADE-4/) for the R environment. It contains Data Analysis functions to analyse Ecological and Environmental data in the framework of Euclidean Exploratory methods, hence the name ade4 (i.e., 4 is not a version number but means that there are four E in the acronym). The ade4 package is available in CRAN, but it can also be used directly online, thanks to the Rweb system (http://pbil.univ-lyon1.fr/Rweb/). This possibility is being used to provide multivariate analysis services in the field of bioinformatics, particularly for sequence and genome structure analysis at the PBIL (http://pbil.univ-lyon1.fr/). An example of these services is the automated analysis of the codon usage of a set of DNA sequences by correspondence analysis ([Perrière et al., 2003] http://pbil.univ-lyon1.fr/mva/coa.php).2 The duality diagram classThe basic tool in ade4 is the duality diagram [Escoufier, 1987]. A duality diagram is simply a list that contains a triplet (X, Q, D): - X is a table with n rows and p columns, considered as p points in Rn (column vectors) or n points in Rp (row vectors). - Q is a p ×p diagonal matrix containing the weights of the p columns of X, and used as a scalar product in Rp (Q is stored under the form of a vector of length p). - D is a n ×n diagonal matrix containing the weights of the n rows of X, and used as a scalar product in Rn (D is stored under the form of a vector of length n). For example, if X is a table containing normalized quantitative variables, if Q is the identity matrix Ip and if D is equal to [1/n]In, the triplet corresponds to a principal component analysis on correlation matrix (normed PCA). Each basic method corresponds to a particular triplet (see table 1), but more complex methods can also be represented by their duality diagram.
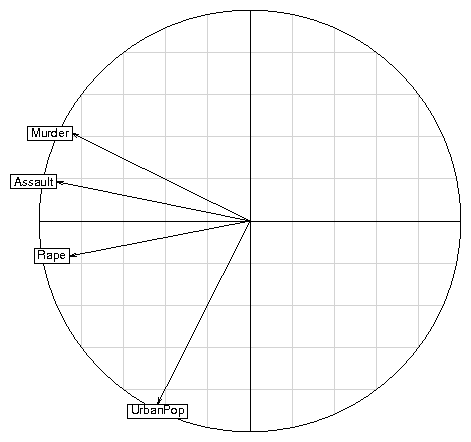
The singular value decomposition of a triplet gives principal axes, principal components, and row and column coordinates, which are added to the triplet for later use. We can use for example a well-known dataset from the base package : data(USArrests) pca1 <- dudi.pca(USArrests, scannf = FALSE, nf = 3)scannf = FALSE means that the number of principal components that will be used to compute row and column coordinates should not be asked interactively to the user, but taken as the value of argument nf (by default, nf = 2). Other parameters allow to choose between centered, normed or raw PCA (default is centered and normed), and to set arbitrary row and column weights. The pca1 object is a duality diagram, i.e., a list made of several vectors and dataframes: pca1 Duality diagramm class: pca dudi $call: dudi.pca(df = USArrests, scannf = FALSE, nf = 3) $nf: 3 axis-components saved $rank: 4 eigen values: 2.48 0.9898 0.3566 0.1734 vector length mode content 1 $cw 4 numeric column weights 2 $lw 50 numeric row weights 3 $eig 4 numeric eigen values data.frame nrow ncol content 1 $tab 50 4 modified array 2 $li 50 3 row coordinates 3 $l1 50 3 row normed scores 4 $co 4 3 column coordinates 5 $c1 4 3 column normed scores other elements: cent normpca1$lw and pca1$cw are the row and column weights that define the duality diagram, together with the data table (pca1$tab). pca1$eig contains the eigenvalues. The row and column coordinates are stored in pca1$li and pca1$co. The variance of these coordinates is equal to the corresponding eigenvalue, and unit variance coordinates are stored in pca1$l1 and pca1$c1 (this is usefull to draw biplots). The general optimization theorems of data analysis take particular meanings for each type of analysis, and graphical functions are proposed to draw the canonical graphs, i.e., the graphical expression corresponding to the mathematical property of the object. For example, the normed PCA of a quantitative variable table gives a score that maximizes the sum of squared correlations with variables. The PCA canonical graph is therefore a graph showing how the sum of squared correlations is maximized for the variables of the data set. On the USArrests example, we obtain the following graphs: score(pca1) s.corcircle(pca1$co) 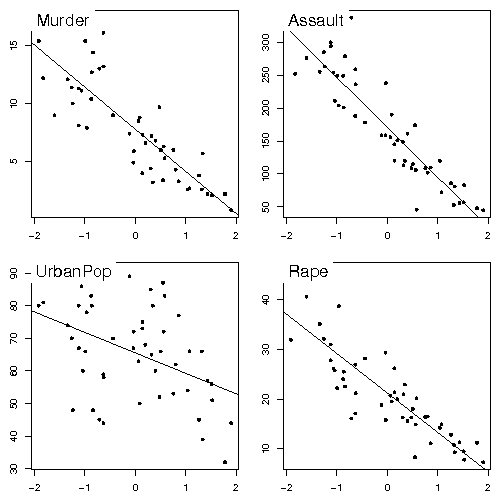
scatter(pca1) 
s.label(pca1$li) 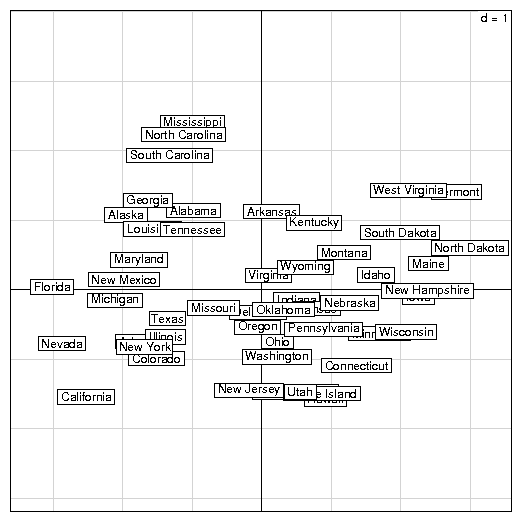
3 Distance matricesA duality diagram can also come from a distance matrix, if this matrix is Euclidean (i.e., if the distances in the matrix are the distances between some points in a Euclidean space). The ade4 package contains functions to compute dissimilarity matrices (dist.binary for binary data, and dist.prop for frequency data), test whether they are Euclidean [Gower and Legendre, 1986], and make them Euclidean (quasieuclid, lingoes, [Lingoes, 1971], cailliez, [Cailliez, 1983]). These functions are useful to ecologists who use the works of [Legendre and Anderson, 1999] and [Legendre and Legendre, 1998]. The Yanomama data set ([Manly, 1991]) contains three distance matrices between 19 villages of Yanomama Indians. The dudi.pco function can be used to compute a principal coordinates analysis (PCO, [Gower, 1966]), that gives a Euclidean representation of the 19 villages. This Euclidean representation allows to compare the geographical, genetic and anthropometric distances.data(yanomama) gen <- quasieuclid(as.dist(yanomama$gen)) geo <- quasieuclid(as.dist(yanomama$geo)) ant <- quasieuclid(as.dist(yanomama$ant)) geo1 <- dudi.pco(geo, scann = FALSE, nf = 3) gen1 <- dudi.pco(gen, scann = FALSE, nf = 3) ant1 <- dudi.pco(ant, scann = FALSE, nf = 3) par(mfrow = c(2, 2)) scatter(geo1) scatter(gen1) scatter(ant1, posi = "bottom") 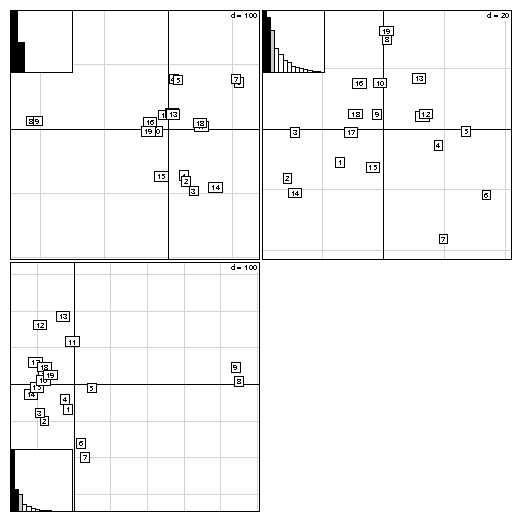
4 Taking into account groups of individualsIn sites x species tables, rows correspond to sites, columns correspond to species, and the values are the number of individuals of species j found at site i. These tables can have many columns and cannot be used in a discriminant analysis. In this case, between-class analyses (between function) are a better alternative, and they can be used with any duality diagram. The between-class analysis of triplet (X, Q, D) for a given factor f is the analysis of the triplet (G, Q, Dw), where G is the table of the means of table X for the groups defined by f, and Dw is the diagonal matrix of group weights. For example, a between-class correspondence analysis (BCA) is very simply obtained after a correspondence analysis (CA):data(meaudret) coa1 <- dudi.coa(meaudret$fau, scannf = FALSE) bet1 <- between(coa1, meaudret$plan$sta, scannf = FALSE) plot(bet1)The meaudret$fau dataframe is an ecological table with 24 rows corresponding to six sampling sites along a small French stream (the Meaudret). These six sampling sites were sampled four times (spring, summer, winter and autumn), hence the 24 rows. The 13 columns correspond to 13 ephemerotera species. The CA of this data table is done with the dudi.coa function, giving the coa1 duality diagram. The corresponding bewteen-class analysis is done with the between function, considering the sites as classes (meaudret$plan$sta is a factor defining the classes). Therefore, this is a between-sites analysis, which aim is to discriminate the sites, given the distribution of ephemeroptera species. This gives the bet1 duality diagram, and Figure 6 shows the graph obtained by plotting this object. 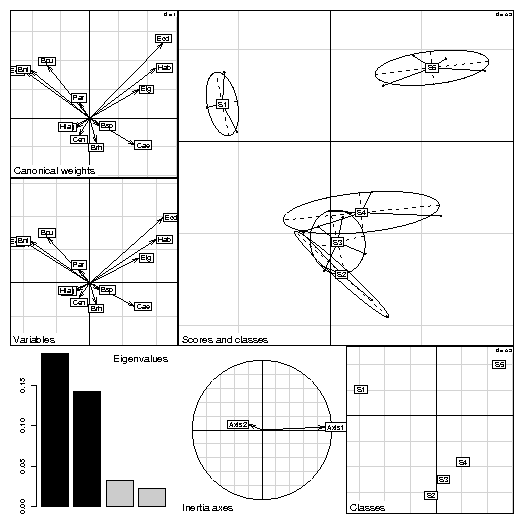
5 Permutation testsPermutation tests (also called Monte-Carlo tests, or randomization tests) can be used to assess the statistical significance of between-class analyses. Many permutation tests are available in the ade4 package, for example mantel.randtest, procuste.randtest, randtest.between, randtest.coinertia, RV.rtest, randtest.discrimin, and several of these tests are available both in R (mantel.rtest) and in C (mantel.randtest) programming langage. The R version allows to see how computations are performed, and to write easily other tests, while the C version is needed for performance reasons. The statistical significance of the BCA can be evaluated with the randtest.between function. By default, 999 permutations are simulated, and the resulting object (test1) can be plotted (Figure 7). The p-value is highly significant, which confirms the existence of differences between sampling sites. The plot shows that the observed value is very far to the right of the histogram of simulated values.test1 <- randtest.between(bet1) test1 Monte-Carlo test Call: randtest.between(xtest = bet1) Observation: 0.4292 Based on 999 replicates Simulated p-value: 0.001 Alternative hypothesis: greater Std.Obs Expectation Variance 3.834237 0.256985 0.002018 plot(test1, main = "Between class inertia") 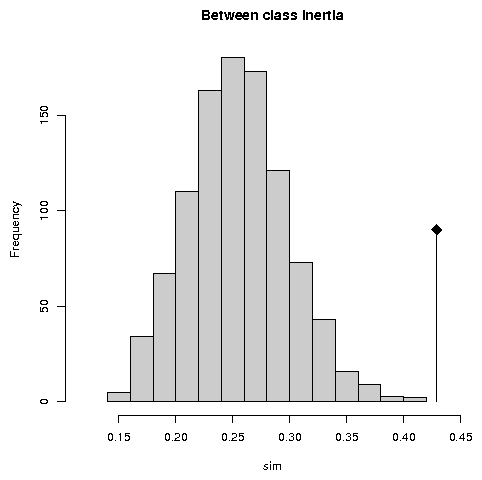
6 ConclusionWe have described only the most basic functions of the ade4 package, considering only the simplest one-table data analysis methods. Many other dudi methods are available in ade4, for example multiple correspondence analysis (dudi.acm), fuzzy correspondence analysis (dudi.fca), analysis of a mixture of numeric variables and factors (dudi.mix), non symmetric correspondence analysis (dudi.nsc), decentered correspondence analysis (dudi.dec). We are preparing a second paper, dealing with two-tables coupling methods, among which canonical correspondence analysis and redundancy analysis are the most frequently used in ecology ([Legendre and Legendre, 1998]). The ade4 package proposes an alternative to these methods, based on the co-inertia criterion ([Dray et al., 2003]). The third category of data analysis methods available in ade4 are K-tables analysis methods, that try to extract the stable part in a series of tables. These methods come from the STATIS strategy, [Lavit et al., 1994] (statis and pta functions) or from the multiple coinertia strategy (mcoa function). The mfa and foucart functions perform two variants of K-tables analysis, and the STATICO method (function ktab.match2ktabs, [Thioulouse et al., 2004]) allows to extract the stable part of species-environment relationships, in time or in space. Methods taking into account spatial constraints (multispati function) and phylogenetic constraints (phylog function) are under development.Bibliography
File translated from TEX by TTH, version 3.67. On 4 Oct 2006, 14:33. |