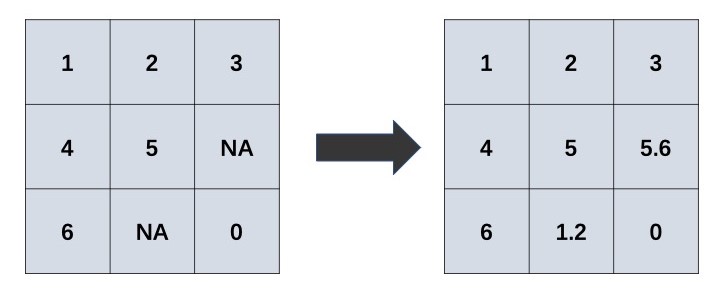
Matrix completion is a procedure for imputing the missing elements in matrices by using the information of observed elements. This procedure can be visualized as:

Matrix completion has attracted a lot of attention, it is widely applied in: - tabular data imputation: recover the missing elements in data table; - recommend system: estimate users’ potantial preference for items pending purchased; - image inpainting: inpaint the missing elements in digit images.
A computationally efficient R package, eimpute is developed for matrix completion.
Install the stable version from CRAN:
install.packages("eimpute")In eimpute, matrix completion problem is solved by iteratively performing low-rank approximation and data calibration, which enjoy two admirable advantages: - unbiased low-rank approximation for incomplete matrix - less time consumption via truncated SVD Moreover, eimpute also supports flexible data standardization.
Compare eimpute and softimpute in systhesis datasets \(X_{m \times m}\) with \(p\) proportion missing observations:
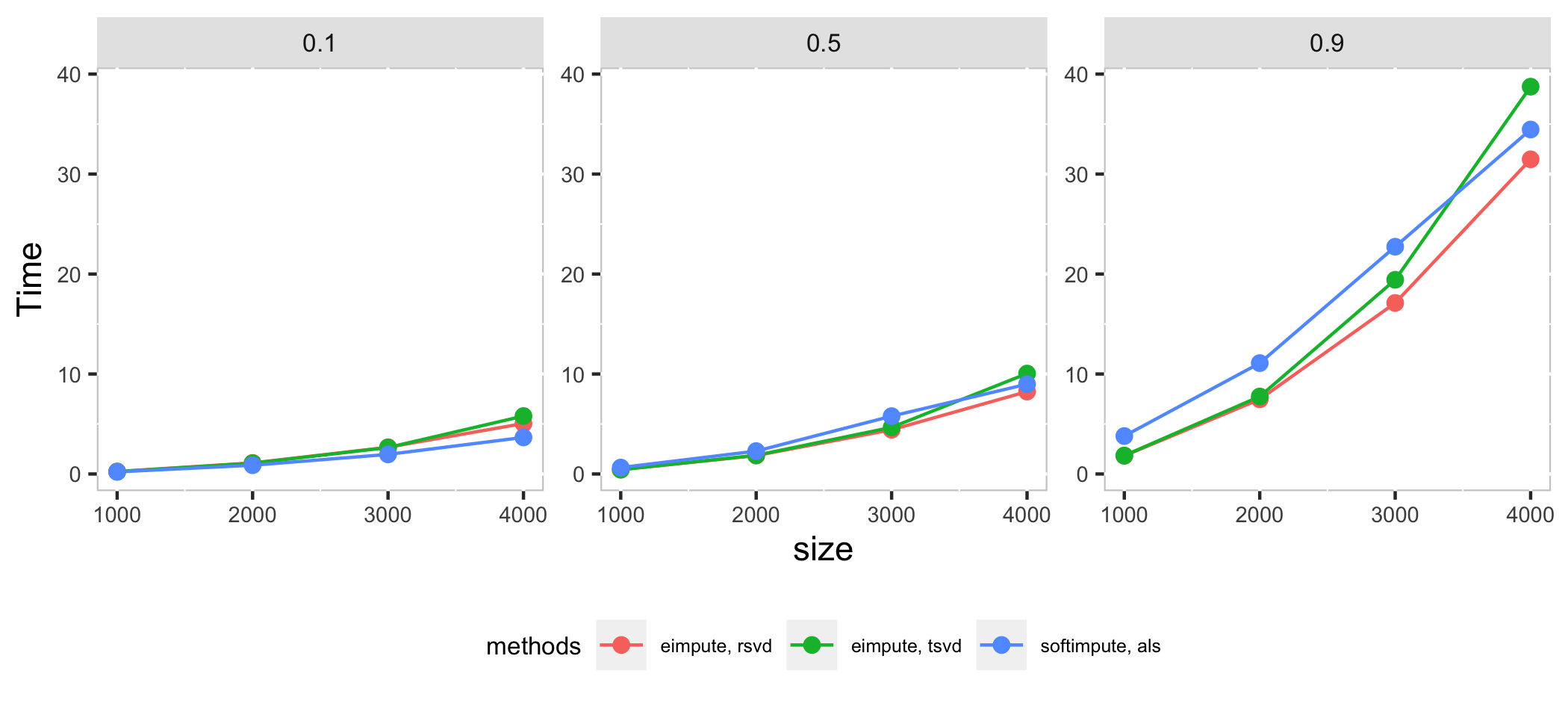
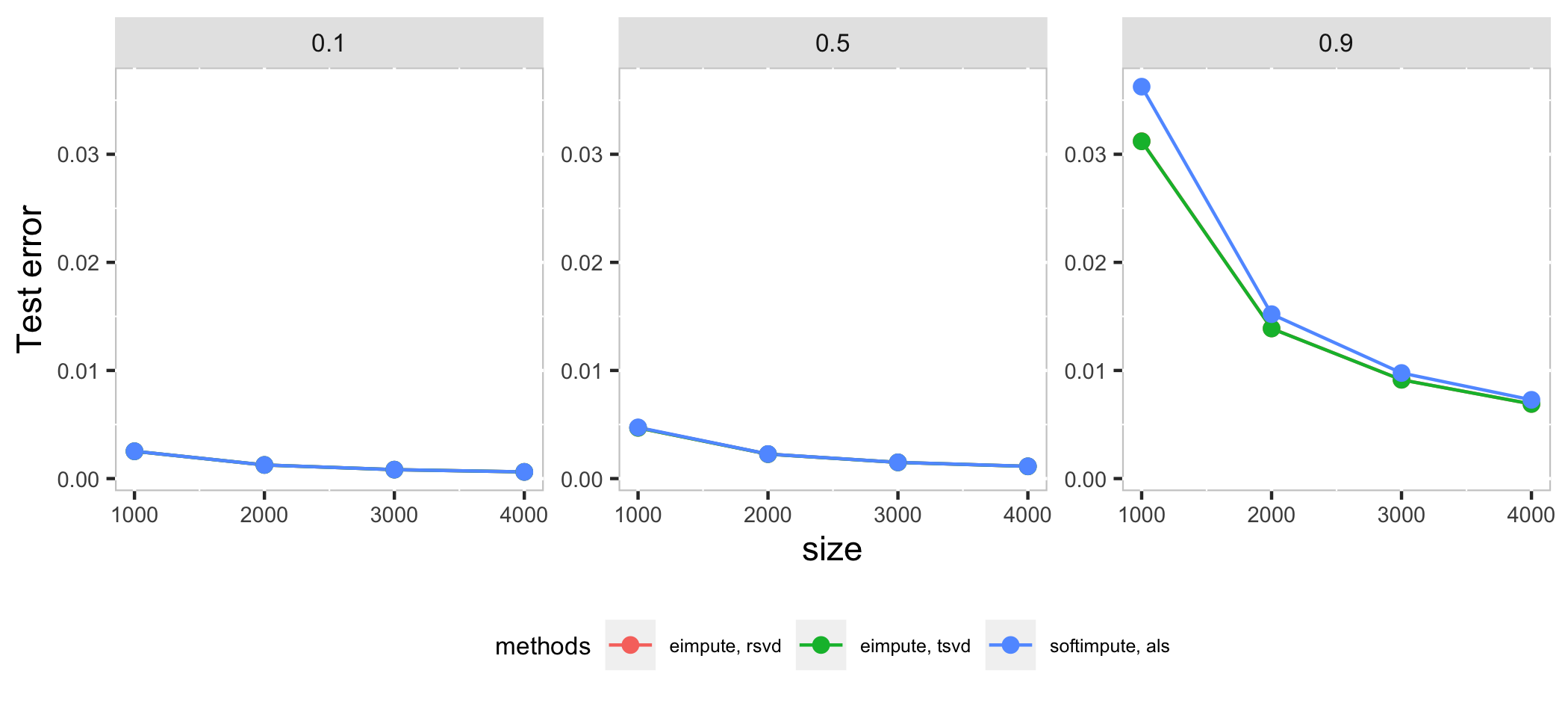
In high dimension case, als method in softimpute is a little faster than eimpute in low proportion of missing observations, as the proportion of missing observations increase, rsvd method in eimpute have a better performance than softimpute in time cost and test error. Compare with two method in **eimpute*, rsvd method is better than tsvd in time cost.
Rahul Mazumder, Trevor Hastie and Rob Tibshirani (2010) Spectra Regularization Algorithms for Learning Large Incomplete Matrices, Journal of Machine Learning Research 11 (2010) 2287-2322
Nathan Halko, Per-Gunnar Martinsson, Joel A. Tropp (2011) Finding Structure with Randomness: Probabilistic Algorithms for Constructing Approximate Matrix Decompositions, SIAM Review Vol. 53, num. 2, pp. 217-288
Send an email to Zhe Gao at gaozh8@mail.ustc.edu.cn