An R package for mixed variable nonlinear optimization
The goal of mixopt is to optimize nonlinear functions that have mixed variable inputs. Both local and global optimization are available.
You can install the development version of mixopt from GitHub with:
# install.packages("devtools")
devtools::install_github("CollinErickson/mixopt")Load the package with the following:
library(mixopt)Suppose you have a function, called f2, that takes in
two arguments. The first is a continuous numeric value between 2 and 8.
The second is a discrete factor that can on the values ‘a’, ‘b’, ‘c’,
‘d’, ‘e’, or ‘f’.
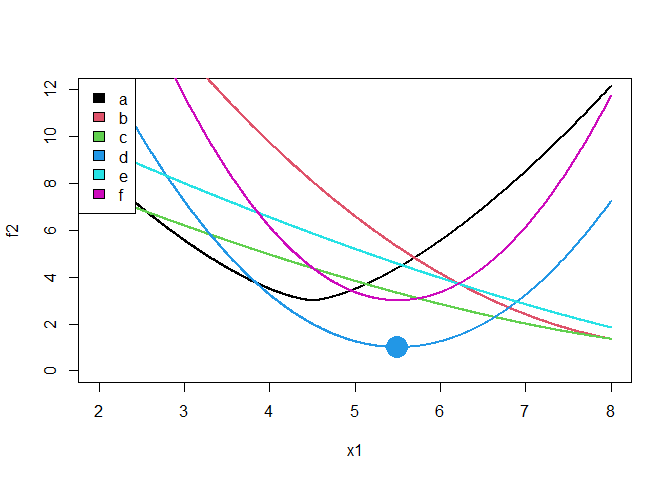
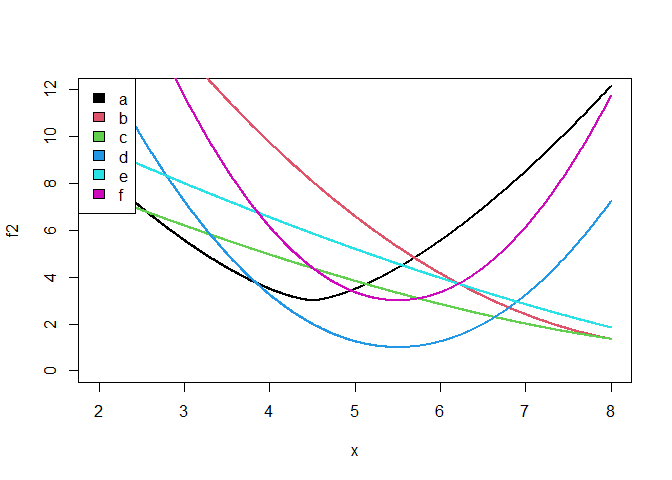
The six lines shown below are how the function varies when varying the first parameter while leaving the second at one of the levels, as indicated in the legend.
To run coordinate descent on this function, we will use
mixopt_coorddesc and need to specify the possible values
for the inputs. To specify a continuous variable from 2 to 8, we use
mopar_cts(2,8). To specify our discrete variable, we can
use mopar_unordered("a", "b", "c", "d", "e", "f"). For this
function, unordered means that there is no ordering over the six factor
options.
We call the function as follows. Note that we have to put our
parameter ranges/values in a list and pass it in to par,
and the function gets passed in to the argument fn.
# Run the optimizer
out <- mixopt_coorddesc(
par=list(
mopar_cts(2,8),
mopar_unordered(letters[1:6])
),
fn=f2,
verbose=0
)
# Print the result
# par is the parameter values
# val is the function value at the minimum
out
#> $par
#> $par[[1]]
#> [1] 5.5
#>
#> $par[[2]]
#> [1] "d"
#>
#>
#> $val
#> [1] 1
#>
#> $counts
#> function gradient
#> 26 NA
#>
#> $runtime
#> Time difference of 0.002993107 secsThe output from the optimizer tells the value, the parameter values, the number of function evaluations made, and the time it took.
The large dot shows where the optimizer ends when using
mixopt_coorddesc. On this problem, it is very likely to get
stuck in a local minimum on the right side since it is doing coordinate
descent. We could get better results using a global optimization
method.