RStanKritian Brock
trialr is a collection of Bayesian clinical trial
designs implemented in Stan and R. The documentation is available at https://brockk.github.io/trialr/
There are many notable Bayesian designs and methods for clinical trials. However, one of the factors that has constrained their use is the availability of software. We present here some of the most popular, implemented and demonstrated in a consistent style, leveraging the powerful Stan environment for Bayesian computing.
Implementations exist in other R packages. Sometimes authors make available code with their publications. However, challenges to use still persist. Different methods are presented in disparate styles. Features implemented in one package for one design may be missing in another. Sometimes the technology chosen may only be available on a particular operating system, or the chosen technology may have fallen into disuse.
trialr seeks to address these problems. Models are
specified in Stan, a state-of-the-art
environment for Bayesian analysis. It uses Hamiltonian Monte Carlo to
take samples from the posterior distribution. This method is more
efficient than Gibbs sampling and reliable inference can usually be
performed on a few thousand posterior samples. R, Stan and
trialr are each available on Mac, Linux, and Windows, so
all of the examples presented here work on each operating system.
Furthermore, Stan offers a very simple method to split the sampling
across n cores, taking full advantage of the modern multicore
processors.
The designs implemented in trialr are introduced briefly
below, and developed more fully in vignettes. We focus on real-life
usage, including:
ggplot
graphics.In all examples, we will need to load trialr
library(trialr)The Continual Reassessment Method (CRM) was first published by O’Quigley, Pepe, and Fisher (1990). It assumes a smooth mathematical form for the dose-toxicity curve to conduct a dose-finding trial seeking a maximum tolerable dose. There are many variations to suit different clinical scenarios and the design has enjoyed relatively common use, although nowhere near as common as the ubiquitous and inferior 3+3 design.
We will demonstrate the method using a notional trial example. In a scenario of five doses, we seek the dose with probability of toxicity closest to 25% where our prior guesses of the rates of toxicity can be represented:
target <- 0.25
skeleton <- c(0.05, 0.15, 0.25, 0.4, 0.6)Let us assume that we have already treated 2 patients each at doses 2, 3 and 4, having seen two toxicities at dose-level 4 and none elsewhere. What dose should we give to the next patient or cohort? We fit the data to the popular empiric variant of the CRM model:
fit1 <- stan_crm(outcome_str = '2NN 3NN 4TT', skeleton = skeleton,
target = target, model = 'empiric', beta_sd = sqrt(1.34),
seed = 123)The parameter outcome_str = '2NN 3NN 4TT' reflects that
two patients each have been treated at doses 2, 3, and 4, and that the
two patients at dose 4 had toxicity but the other patients did not.
The fitted model contains lots of useful of information:
fit1
#> Patient Dose Toxicity Weight
#> 1 1 2 0 1
#> 2 2 2 0 1
#> 3 3 3 0 1
#> 4 4 3 0 1
#> 5 5 4 1 1
#> 6 6 4 1 1
#>
#> Dose Skeleton N Tox ProbTox MedianProbTox ProbMTD
#> 1 1 0.05 0 0 0.108 0.0726 0.2140
#> 2 2 0.15 2 0 0.216 0.1900 0.2717
#> 3 3 0.25 2 0 0.310 0.2972 0.2657
#> 4 4 0.40 2 2 0.444 0.4484 0.2090
#> 5 5 0.60 0 0 0.624 0.6395 0.0395
#>
#> The model targets a toxicity level of 0.25.
#> The dose with estimated toxicity probability closest to target is 2.
#> The dose most likely to be the MTD is 2.
#> Model entropy: 1.49library(ggplot2)
library(tidybayes)
library(dplyr)
fit1 %>%
spread_draws(prob_tox[Dose]) %>%
ggplot(aes(x = Dose, y = prob_tox)) +
stat_interval(.width = c(.5, .8, .95)) +
scale_color_brewer() +
labs(y = 'Prob(DLT)', title = 'Posterior dose-toxicity beliefs using empiric CRM')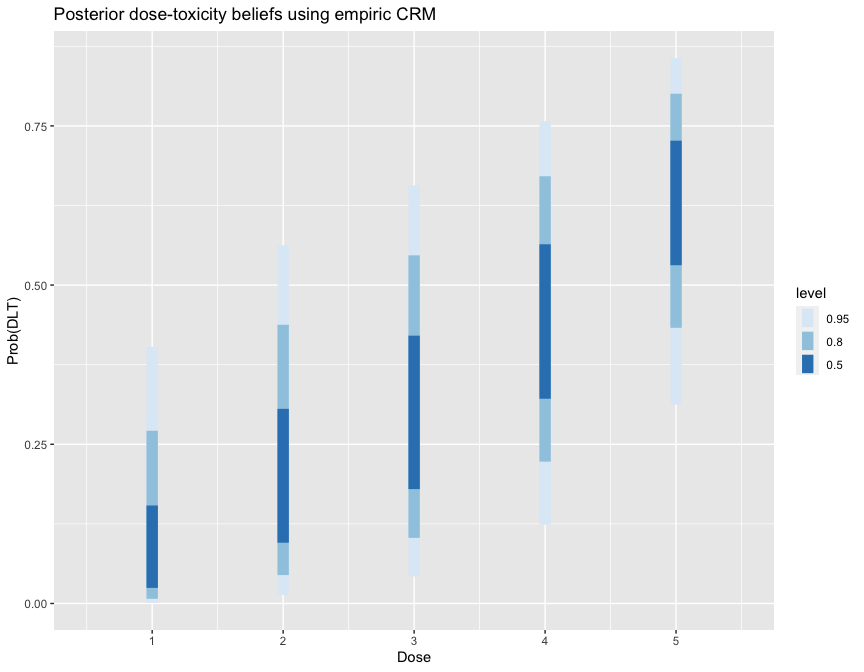
Several variants of the CRM are implemented in ‘trialr’. These are demonstrated in the CRM vignette. Several visualisation techniques are illustrated in the Visualisation in CRM vignette. The time-to-event CRM is introduced in the TITE-CRM vignette.
Neuenschwander, Branson, and Gsponer (2008) introduced a two-parameter logistic model for dose-escalation. It shares many characteristics of the CRM models presented above but instead of a skeleton, it uses as a covariate the doses under investigation divided by some reference dose.
E.g., reproducing one of the analyses in their paper:
dose <- c(1, 2.5, 5, 10, 15, 20, 25, 30, 40, 50, 75, 100, 150, 200, 250)
d_star <- 250
target <- 0.30
outcomes <- '1NNN 2NNNN 3NNNN 4NNNN 7TT'
fit <- stan_nbg(outcome_str = outcomes, real_doses = dose, d_star = d_star,
target = target, alpha_mean = 2.15, alpha_sd = 0.84,
beta_mean = 0.52, beta_sd = 0.8, seed = 2020, refresh = 0)
fit
#> Patient Dose Toxicity Weight
#> 1 1 1 0 1
#> 2 2 1 0 1
#> 3 3 1 0 1
#> 4 4 2 0 1
#> 5 5 2 0 1
#> 6 6 2 0 1
#> 7 7 2 0 1
#> 8 8 3 0 1
#> 9 9 3 0 1
#> 10 10 3 0 1
#> 11 11 3 0 1
#> 12 12 4 0 1
#> 13 13 4 0 1
#> 14 14 4 0 1
#> 15 15 4 0 1
#> 16 16 7 1 1
#> 17 17 7 1 1
#>
#> Dose N Tox ProbTox MedianProbTox ProbMTD
#> 1 1 3 0 0.0126 0.00563 0.00025
#> 2 2 4 0 0.0325 0.01967 0.00050
#> 3 3 4 0 0.0675 0.04934 0.02250
#> 4 4 4 0 0.1385 0.11863 0.10450
#> 5 5 0 0 0.2064 0.18937 0.16775
#> 6 6 0 0 0.2692 0.25641 0.17100
#> 7 7 2 2 0.3264 0.31878 0.14425
#> 8 8 0 0 0.3780 0.37409 0.16850
#> 9 9 0 0 0.4661 0.46884 0.12475
#> 10 10 0 0 0.5371 0.54698 0.07125
#> 11 11 0 0 0.6616 0.67700 0.02000
#> 12 12 0 0 0.7390 0.75753 0.00375
#> 13 13 0 0 0.8259 0.84691 0.00075
#> 14 14 0 0 0.8717 0.89297 0.00025
#> 15 15 0 0 0.8993 0.91986 0.00000
#>
#> The model targets a toxicity level of 0.3.
#> The dose with estimated toxicity probability closest to target is 7.
#> The dose most likely to be the MTD is 6.
#> Model entropy: 2.06This reproduces the inferences depicted in the lower right pane of Figure 1 in Neuenschwander, Branson, and Gsponer (2008).
For more, see the Two-parameter logistic model for dose-finding by Neuenschwander, Branson & Gsponer vignette.
EffTox by Thall and Cook (2004) is a dose-finding design that uses binary efficacy and toxicity outcomes to select a dose with a high utility score. We present it briefly here but there is a much more thorough examination in the EffTox vignette.
For demonstration, we fit the model parameterisation introduced by Thall et al. (2014) to the following notional outcomes:
| Patient | Dose-level | Toxicity | Efficacy |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 0 | 1 |
| 4 | 2 | 0 | 1 |
| 5 | 2 | 0 | 1 |
| 6 | 2 | 1 | 1 |
outcomes <- '1NNE 2EEB'
fit2 <- stan_efftox_demo(outcomes, seed = 123)In an efficacy and toxicity dose-finding scenario, the number of patient outcomes has increased. It is possible that patients experience efficacy only (E), toxicity only (T), both (B) or neither (N).
fit2
#> Patient Dose Toxicity Efficacy
#> 1 1 1 0 0
#> 2 2 1 0 0
#> 3 3 1 0 1
#> 4 4 2 0 1
#> 5 5 2 0 1
#> 6 6 2 1 1
#>
#> Dose N ProbEff ProbTox ProbAccEff ProbAccTox Utility Acceptable ProbOBD
#> 1 1 3 0.402 0.088 0.333 0.927 -0.342 TRUE 0.0465
#> 2 2 3 0.789 0.103 0.943 0.921 0.412 TRUE 0.2625
#> 3 3 0 0.929 0.225 0.984 0.718 0.506 TRUE 0.2077
#> 4 4 0 0.955 0.315 0.983 0.617 0.420 FALSE 0.0620
#> 5 5 0 0.964 0.372 0.980 0.561 0.349 FALSE 0.4213
#>
#> The model recommends selecting dose-level 3.
#> The dose most likely to be the OBD is 5.
#> Model entropy: 1.36In this example, after evaluation of our six patients, the dose advocated for the next group is dose-level 3. This is contained in the fitted object:
fit2$recommended_dose
#> [1] 3This is not surprising because dose 3 has the highest utility score:
fit2$utility
#> [1] -0.3418428 0.4120858 0.5064312 0.4199298 0.3493254Sometimes, doses other than the maximal-utility dose will be recommended because of the dose-admissibility rules. See the EffTox vignette and the original papers for more details.
Functions are provided to create useful plots. For instance, it is illuminating to plot the posterior means of the probabilities of efficacy and toxicity at each of the doses on the trade-off contours used to measure dose attractiveness. The five doses are shown in red. Doses closer to the lower-right corner have higher utility.
efftox_contour_plot(fit2)
title('EffTox utility contours')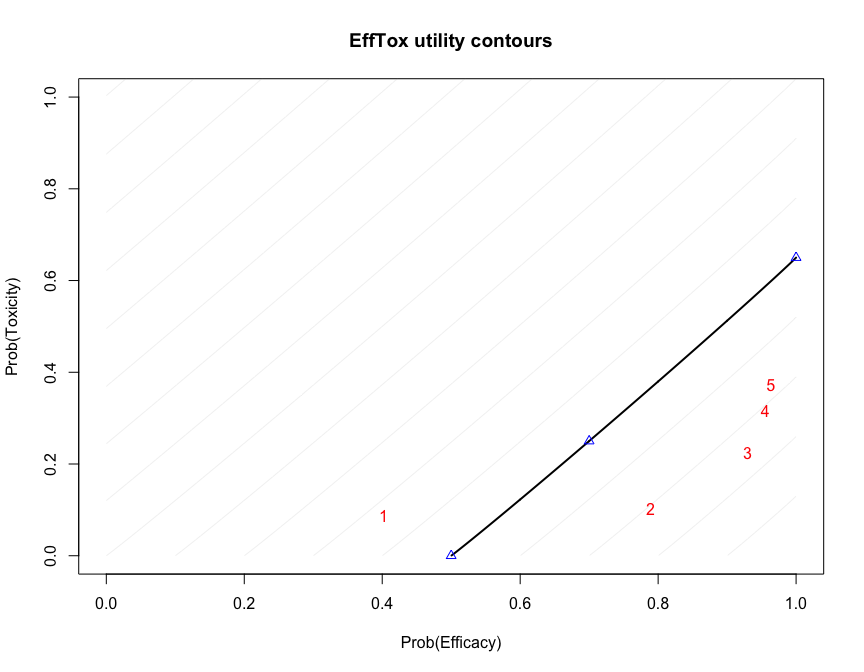
This example continues in the EffTox vignette. There are many publications related to EffTox, including Thall and Cook (2004) and Thall et al. (2014).
Sticking with Peter Thall’s huge contribution to Bayesian clinical trials, Thall et al. (2003) described a method for analysing treatment effects of a single intervention in several sub-types of a single disease.
We demonstrate the method for partially-pooling response rates to a single drug in various subtypes of sarcoma. This example is used in Thall et al. (2003). Fitting the data to the model:
fit3 <- stan_hierarchical_response_thall(
group_responses = c(0, 0, 1, 3, 5, 0, 1, 2, 0, 0),
group_sizes = c(0, 2 ,1, 7, 5, 0, 2, 3, 1, 0),
mu_mean = -1.3863,
mu_sd = sqrt(1 / 0.1),
tau_alpha = 2,
tau_beta = 20)mu and tau are mean and precision
parameters for the partially-pooled effects in the model.
mu_mean and mu_sd are hyperparameters for a
normal prior, and tau_alpha and tau_beta are
hyperparameters for an inverse gamma prior. This specification is
described in the original model.
The returned object is the same type as the fits returned by rstan:
fit3
#> Inference for Stan model: ThallHierarchicalBinary.
#> 4 chains, each with iter=2000; warmup=1000; thin=1;
#> post-warmup draws per chain=1000, total post-warmup draws=4000.
#>
#> mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff
#> mu -0.04 0.03 1.38 -2.86 -0.89 -0.02 0.86 2.60 2295
#> sigma2 13.22 0.59 16.18 3.45 6.44 9.56 14.77 43.41 748
#> rho[1] -0.03 0.07 3.87 -8.25 -2.26 0.08 2.29 7.20 3079
#> rho[2] -3.03 0.06 2.63 -9.68 -4.20 -2.55 -1.31 0.69 1899
#> rho[3] 2.46 0.07 2.86 -1.87 0.65 2.06 3.83 9.13 1497
#> rho[4] -0.31 0.01 0.79 -1.87 -0.82 -0.31 0.21 1.22 4031
#> rho[5] 3.76 0.06 2.42 0.59 2.11 3.31 4.78 10.04 1448
#> rho[6] -0.09 0.07 3.85 -8.34 -2.27 0.02 2.27 7.41 3092
#> rho[7] 0.06 0.03 1.53 -2.90 -0.92 0.09 0.99 3.05 3658
#> rho[8] 0.75 0.02 1.31 -1.55 -0.12 0.65 1.52 3.65 2785
#> rho[9] -2.43 0.07 2.91 -9.18 -3.86 -2.00 -0.50 2.09 1919
#> rho[10] 0.01 0.07 3.97 -7.85 -2.29 0.05 2.38 7.74 2982
#> sigma 3.38 0.05 1.33 1.86 2.54 3.09 3.84 6.59 819
#> prob_response[1] 0.50 0.01 0.38 0.00 0.09 0.52 0.91 1.00 3476
#> prob_response[2] 0.15 0.00 0.18 0.00 0.01 0.07 0.21 0.67 3817
#> prob_response[3] 0.78 0.00 0.25 0.13 0.66 0.89 0.98 1.00 4141
#> prob_response[4] 0.43 0.00 0.17 0.13 0.31 0.42 0.55 0.77 4036
#> prob_response[5] 0.92 0.00 0.10 0.64 0.89 0.96 0.99 1.00 3879
#> prob_response[6] 0.50 0.01 0.38 0.00 0.09 0.51 0.91 1.00 3564
#> prob_response[7] 0.51 0.00 0.27 0.05 0.28 0.52 0.73 0.95 3642
#> prob_response[8] 0.64 0.00 0.22 0.18 0.47 0.66 0.82 0.97 3040
#> prob_response[9] 0.23 0.00 0.26 0.00 0.02 0.12 0.38 0.89 3971
#> prob_response[10] 0.50 0.01 0.38 0.00 0.09 0.51 0.92 1.00 2970
#> lp__ -34.42 0.15 3.77 -43.20 -36.48 -33.86 -31.71 -28.88 611
#> Rhat
#> mu 1
#> sigma2 1
#> rho[1] 1
#> rho[2] 1
#> rho[3] 1
#> rho[4] 1
#> rho[5] 1
#> rho[6] 1
#> rho[7] 1
#> rho[8] 1
#> rho[9] 1
#> rho[10] 1
#> sigma 1
#> prob_response[1] 1
#> prob_response[2] 1
#> prob_response[3] 1
#> prob_response[4] 1
#> prob_response[5] 1
#> prob_response[6] 1
#> prob_response[7] 1
#> prob_response[8] 1
#> prob_response[9] 1
#> prob_response[10] 1
#> lp__ 1
#>
#> Samples were drawn using NUTS(diag_e) at Thu Oct 15 09:52:56 2020.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
#> convergence, Rhat=1).So, we can use the underlying plot method in rstan.
library(rstan)
library(ggplot2)
plot(fit3, pars = 'prob_response') +
geom_vline(xintercept = 0.3, col = 'orange', linetype = 'dashed') +
labs(title = 'Partially-pooled response rates in 10 sarcoma subtypes')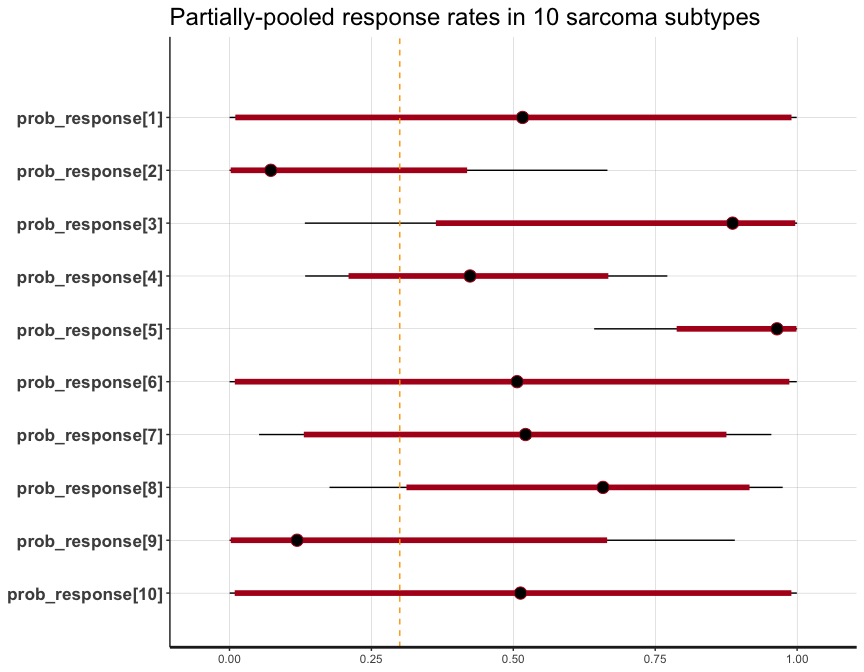
The hierarchical model for binary responses is developed in its own vignette.
Thall, Nguyen, and Estey (2008) introduced an extension of EffTox that allows dose-finding by efficacy and toxicity outcomes and adjusts for covariate information. Brock, et al. (manuscript accepted but not yet in press) simplified the method by removing the dose-finding components to leave a design that studies associated co-primary and toxicity outcomes in an arbitrary number of cohorts determined by the basline covariates. They refered to the simplifed design as BEBOP, for Bayesian Evaluation of Bivariate binary Outcomes with Predictive variables.
The investigators implement the design is a phase II trial of pembrolizumab in non-small-cell lung cancer. A distinct feature of the trial is the availability of predictive baseline covariates, the most noteworthy of which is the PD-L1 tumour proportion score, shown by Garon et al. (2015) to be a predictive biomarker for drug efficacy.
This example is demonstrated in the BEBOP vignette.
You can install the latest trialr commit from github with:
# install.packages("devtools")
devtools::install_github("brockk/trialr")You can install the latest CRAN release by running:
install.packages("trialr")It should go without saying that the CRAN release will be older than the github version.
If there is a published Bayesian design you want implemented in Stan, get in touch. Contact brockk on github.
Garon, Edward B, Naiyer a Rizvi, Rina Hui, Natasha Leighl, Ani S Balmanoukian, Joseph Paul Eder, Amita Patnaik, et al. 2015. “Pembrolizumab for the Treatment of Non-Small-Cell Lung Cancer.” The New England Journal of Medicine 372 (21): 2018–28. https://doi.org/10.1056/NEJMoa1501824.
Neuenschwander, Beat, Michael Branson, and Thomas Gsponer. 2008. “Critical Aspects of the Bayesian Approach to Phase I Cancer Trials.” Statistics in Medicine 27 (13): 2420–39. https://doi.org/10.1002/sim.3230.
O’Quigley, J, M Pepe, and L Fisher. 1990. “Continual Reassessment Method: A Practical Design for Phase 1 Clinical Trials in Cancer.” Biometrics 46 (1): 33–48. https://doi.org/10.2307/2531628.
Thall, Peter F., Hoang Q. Nguyen, and Elihu H. Estey. 2008. “Patient-Specific Dose Finding Based on Bivariate Outcomes and Covariates.” Biometrics 64 (4): 1126–36. https://doi.org/10.1111/j.1541-0420.2008.01009.x.
Thall, Peter F., J. Kyle Wathen, B. Nebiyou Bekele, Richard E. Champlin, Laurence H. Baker, and Robert S. Benjamin. 2003. “Hierarchical Bayesian Approaches to Phase II Trials in Diseases with Multiple Subtypes.” Statistics in Medicine 22 (5): 763–80. https://doi.org/10.1002/sim.1399.
Thall, PF, and JD Cook. 2004. “Dose-Finding Based on Efficacy-Toxicity Trade-Offs.” Biometrics 60 (3): 684–93.
Thall, PF, RC Herrick, HQ Nguyen, JJ Venier, and JC Norris. 2014. “Effective Sample Size for Computing Prior Hyperparameters in Bayesian Phase I-II Dose-Finding.” Clinical Trials 11 (6): 657–66. https://doi.org/10.1177/1740774514547397.